This is the original problem.4x2 – 2x – 5 = 0Move the loose number over to the other side.4x2 – 2x = 5Divide through by whatever is multiplied on the squared term.
Take half of the coefficient (don't forget the sign!) of the x-term, and square it. Add this square to both sides of the equation.
Convert the left-hand side to squared form, and simplify the right-hand side. (This is where you use that sign that you kept track of earlier. You plug it into the middle of the parenthetical part.)
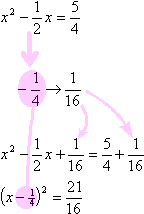Square-root both sides, remembering the"±" on the right-hand side. Simplify as necessary.
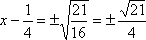Solve for "x =".
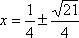Remember that the "±" means that you have two values for x.
Take half of the coefficient (don't forget the sign!) of the x-term, and square it. Add this square to both sides of the equation.
Convert the left-hand side to squared form, and simplify the right-hand side. (This is where you use that sign that you kept track of earlier. You plug it into the middle of the parenthetical part.)
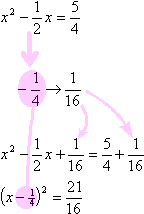Square-root both sides, remembering the"±" on the right-hand side. Simplify as necessary.Solve for "x =".Remember that the "±" means that you have two values for x.
No comments:
Post a Comment